STUMPY documentation#

STUMPY#
STUMPY is a powerful and scalable Python library that efficiently computes something called the matrix profile, which is just an academic way of saying “for every (green) subsequence within your time series, automatically identify its corresponding nearest-neighbor (grey)”:
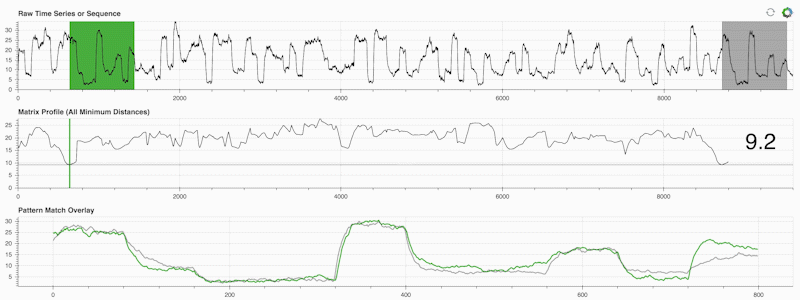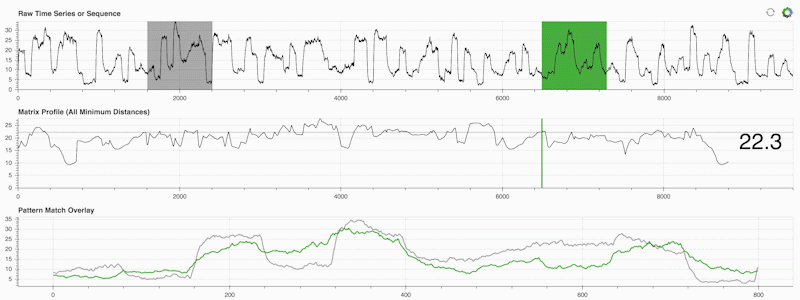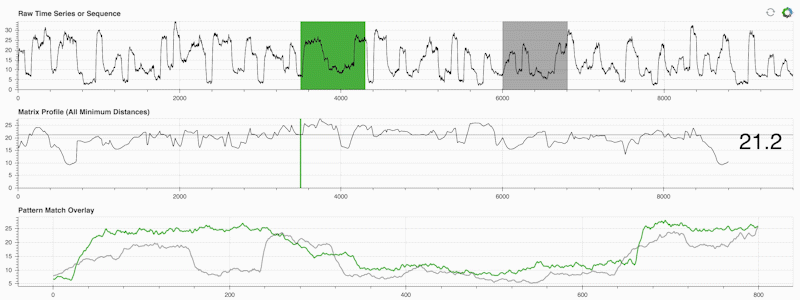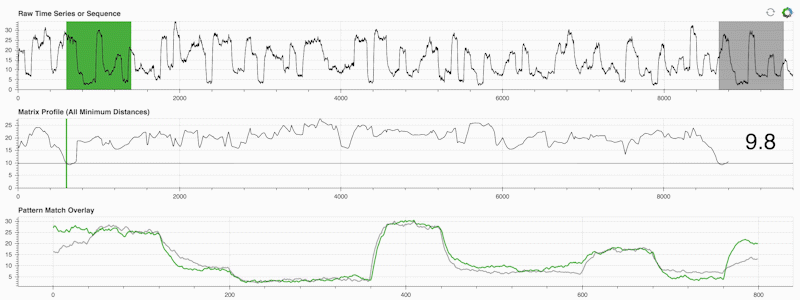
What’s important is that once you’ve computed your matrix profile (middle panel above) it can then be used for a variety of time series data mining tasks such as:
pattern/motif (approximately repeated subsequences within a longer time series) discovery
anomaly/novelty (discord) discovery
shapelet discovery
semantic segmentation
streaming (on-line) data
fast approximate matrix profiles
time series chains (temporally ordered set of subsequence patterns)
snippets for summarizing long time series
pan matrix profiles for selecting the best subsequence window size(s)
Whether you are an academic, data scientist, software developer, or time series enthusiast, STUMPY is straightforward to install and our goal is to allow you to get to your time series insights faster. See documentation for more information.
How to use STUMPY#
Please see our API documentation for a complete list of available functions and see our informative tutorials for more comprehensive example use cases. Below, you will find code snippets that quickly demonstrate how to use STUMPY.
Typical usage (1-dimensional time series data) with STUMP:
import stumpy
import numpy as np
if __name__ == "__main__":
your_time_series = np.random.rand(10000)
window_size = 50 # Approximately, how many data points might be found in a pattern
matrix_profile = stumpy.stump(your_time_series, m=window_size)
Distributed usage for 1-dimensional time series data with Dask Distributed via STUMPED:
import stumpy
import numpy as np
from dask.distributed import Client
if __name__ == "__main__":
with Client() as dask_client:
your_time_series = np.random.rand(10000)
window_size = 50 # Approximately, how many data points might be found in a pattern
matrix_profile = stumpy.stumped(dask_client, your_time_series, m=window_size)
GPU usage for 1-dimensional time series data with GPU-STUMP:
import stumpy
import numpy as np
from numba import cuda
if __name__ == "__main__":
your_time_series = np.random.rand(10000)
window_size = 50 # Approximately, how many data points might be found in a pattern
all_gpu_devices = [device.id for device in cuda.list_devices()] # Get a list of all available GPU devices
matrix_profile = stumpy.gpu_stump(your_time_series, m=window_size, device_id=all_gpu_devices)
Multi-dimensional time series data with MSTUMP:
import stumpy
import numpy as np
if __name__ == "__main__":
your_time_series = np.random.rand(3, 1000) # Each row represents data from a different dimension while each column represents data from the same dimension
window_size = 50 # Approximately, how many data points might be found in a pattern
matrix_profile, matrix_profile_indices = stumpy.mstump(your_time_series, m=window_size)
Distributed multi-dimensional time series data analysis with Dask Distributed MSTUMPED:
import stumpy
import numpy as np
from dask.distributed import Client
if __name__ == "__main__":
with Client() as dask_client:
your_time_series = np.random.rand(3, 1000) # Each row represents data from a different dimension while each column represents data from the same dimension
window_size = 50 # Approximately, how many data points might be found in a pattern
matrix_profile, matrix_profile_indices = stumpy.mstumped(dask_client, your_time_series, m=window_size)
Time Series Chains with Anchored Time Series Chains (ATSC):
import stumpy
import numpy as np
if __name__ == "__main__":
your_time_series = np.random.rand(10000)
window_size = 50 # Approximately, how many data points might be found in a pattern
matrix_profile = stumpy.stump(your_time_series, m=window_size)
left_matrix_profile_index = matrix_profile[:, 2]
right_matrix_profile_index = matrix_profile[:, 3]
idx = 10 # Subsequence index for which to retrieve the anchored time series chain for
anchored_chain = stumpy.atsc(left_matrix_profile_index, right_matrix_profile_index, idx)
all_chain_set, longest_unanchored_chain = stumpy.allc(left_matrix_profile_index, right_matrix_profile_index)
Semantic Segmentation with Fast Low-cost Unipotent Semantic Segmentation (FLUSS):
import stumpy
import numpy as np
if __name__ == "__main__":
your_time_series = np.random.rand(10000)
window_size = 50 # Approximately, how many data points might be found in a pattern
matrix_profile = stumpy.stump(your_time_series, m=window_size)
subseq_len = 50
correct_arc_curve, regime_locations = stumpy.fluss(matrix_profile[:, 1],
L=subseq_len,
n_regimes=2,
excl_factor=1
)
Dependencies#
Supported Python and NumPy versions are determined according to the NEP 29 deprecation policy.
Where to get it#
Conda install (preferred):
conda install -c conda-forge stumpy
PyPI install, presuming you have numpy, scipy, and numba installed:
python -m pip install stumpy
To install stumpy from source, see the instructions in the documentation.
Documentation#
In order to fully understand and appreciate the underlying algorithms and applications, it is imperative that you read the original publications. For a more detailed example of how to use STUMPY please consult the latest documentation or explore our hands-on tutorials.
Performance#
We tested the performance of computing the exact matrix profile using the Numba JIT compiled version of the code on randomly generated time series data with various lengths (i.e., np.random.rand(n)) along with different CPU and GPU hardware resources.
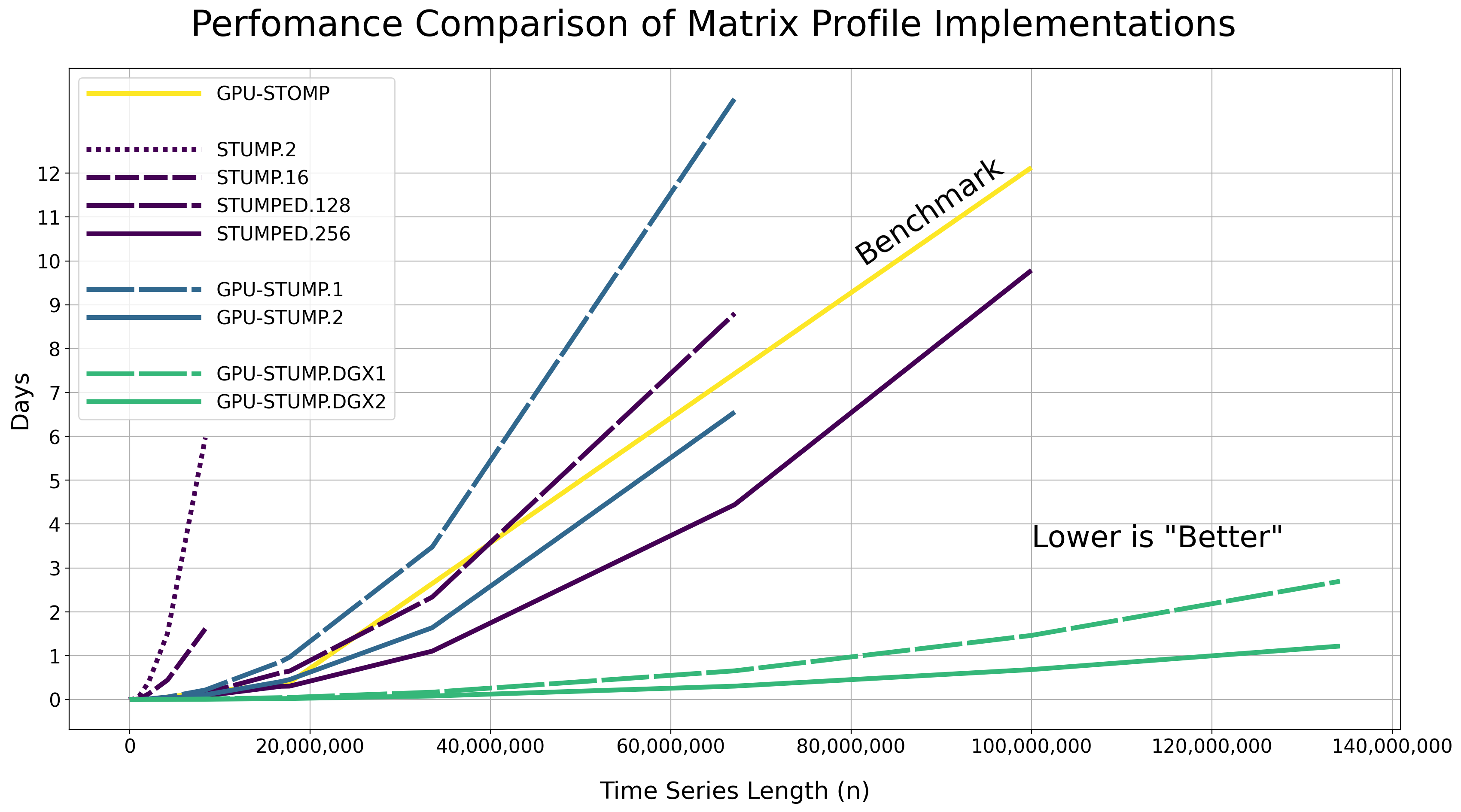
The raw results are displayed in the table below as Hours:Minutes:Seconds.Milliseconds and with a constant window size of m = 50. Note that these reported runtimes include the time that it takes to move the data from the host to all of the GPU device(s). You may need to scroll to the right side of the table in order to see all of the runtimes.
i |
n = 2i |
GPU-STOMP |
STUMP.2 |
STUMP.16 |
STUMPED.128 |
STUMPED.256 |
GPU-STUMP.1 |
GPU-STUMP.2 |
GPU-STUMP.DGX1 |
GPU-STUMP.DGX2 |
|---|---|---|---|---|---|---|---|---|---|---|
6 |
64 |
00:00:10.00 |
00:00:00.00 |
00:00:00.00 |
00:00:05.77 |
00:00:06.08 |
00:00:00.03 |
00:00:01.63 |
NaN |
NaN |
7 |
128 |
00:00:10.00 |
00:00:00.00 |
00:00:00.00 |
00:00:05.93 |
00:00:07.29 |
00:00:00.04 |
00:00:01.66 |
NaN |
NaN |
8 |
256 |
00:00:10.00 |
00:00:00.00 |
00:00:00.01 |
00:00:05.95 |
00:00:07.59 |
00:00:00.08 |
00:00:01.69 |
00:00:06.68 |
00:00:25.68 |
9 |
512 |
00:00:10.00 |
00:00:00.00 |
00:00:00.02 |
00:00:05.97 |
00:00:07.47 |
00:00:00.13 |
00:00:01.66 |
00:00:06.59 |
00:00:27.66 |
10 |
1024 |
00:00:10.00 |
00:00:00.02 |
00:00:00.04 |
00:00:05.69 |
00:00:07.64 |
00:00:00.24 |
00:00:01.72 |
00:00:06.70 |
00:00:30.49 |
11 |
2048 |
NaN |
00:00:00.05 |
00:00:00.09 |
00:00:05.60 |
00:00:07.83 |
00:00:00.53 |
00:00:01.88 |
00:00:06.87 |
00:00:31.09 |
12 |
4096 |
NaN |
00:00:00.22 |
00:00:00.19 |
00:00:06.26 |
00:00:07.90 |
00:00:01.04 |
00:00:02.19 |
00:00:06.91 |
00:00:33.93 |
13 |
8192 |
NaN |
00:00:00.50 |
00:00:00.41 |
00:00:06.29 |
00:00:07.73 |
00:00:01.97 |
00:00:02.49 |
00:00:06.61 |
00:00:33.81 |
14 |
16384 |
NaN |
00:00:01.79 |
00:00:00.99 |
00:00:06.24 |
00:00:08.18 |
00:00:03.69 |
00:00:03.29 |
00:00:07.36 |
00:00:35.23 |
15 |
32768 |
NaN |
00:00:06.17 |
00:00:02.39 |
00:00:06.48 |
00:00:08.29 |
00:00:07.45 |
00:00:04.93 |
00:00:07.02 |
00:00:36.09 |
16 |
65536 |
NaN |
00:00:22.94 |
00:00:06.42 |
00:00:07.33 |
00:00:09.01 |
00:00:14.89 |
00:00:08.12 |
00:00:08.10 |
00:00:36.54 |
17 |
131072 |
00:00:10.00 |
00:01:29.27 |
00:00:19.52 |
00:00:09.75 |
00:00:10.53 |
00:00:29.97 |
00:00:15.42 |
00:00:09.45 |
00:00:37.33 |
18 |
262144 |
00:00:18.00 |
00:05:56.50 |
00:01:08.44 |
00:00:33.38 |
00:00:24.07 |
00:00:59.62 |
00:00:27.41 |
00:00:13.18 |
00:00:39.30 |
19 |
524288 |
00:00:46.00 |
00:25:34.58 |
00:03:56.82 |
00:01:35.27 |
00:03:43.66 |
00:01:56.67 |
00:00:54.05 |
00:00:19.65 |
00:00:41.45 |
20 |
1048576 |
00:02:30.00 |
01:51:13.43 |
00:19:54.75 |
00:04:37.15 |
00:03:01.16 |
00:05:06.48 |
00:02:24.73 |
00:00:32.95 |
00:00:46.14 |
21 |
2097152 |
00:09:15.00 |
09:25:47.64 |
03:05:07.64 |
00:13:36.51 |
00:08:47.47 |
00:20:27.94 |
00:09:41.43 |
00:01:06.51 |
00:01:02.67 |
22 |
4194304 |
NaN |
36:12:23.74 |
10:37:51.21 |
00:55:44.43 |
00:32:06.70 |
01:21:12.33 |
00:38:30.86 |
00:04:03.26 |
00:02:23.47 |
23 |
8388608 |
NaN |
143:16:09.94 |
38:42:51.42 |
03:33:30.53 |
02:00:49.37 |
05:11:44.45 |
02:33:14.60 |
00:15:46.26 |
00:08:03.76 |
24 |
16777216 |
NaN |
NaN |
NaN |
14:39:11.99 |
07:13:47.12 |
20:43:03.80 |
09:48:43.42 |
01:00:24.06 |
00:29:07.84 |
NaN |
17729800 |
09:16:12.00 |
NaN |
NaN |
15:31:31.75 |
07:18:42.54 |
23:09:22.43 |
10:54:08.64 |
01:07:35.39 |
00:32:51.55 |
25 |
33554432 |
NaN |
NaN |
NaN |
56:03:46.81 |
26:27:41.29 |
83:29:21.06 |
39:17:43.82 |
03:59:32.79 |
01:54:56.52 |
26 |
67108864 |
NaN |
NaN |
NaN |
211:17:37.60 |
106:40:17.17 |
328:58:04.68 |
157:18:30.50 |
15:42:15.94 |
07:18:52.91 |
NaN |
100000000 |
291:07:12.00 |
NaN |
NaN |
NaN |
234:51:35.39 |
NaN |
NaN |
35:03:44.61 |
16:22:40.81 |
27 |
134217728 |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
64:41:55.09 |
29:13:48.12 |
Hardware Resources#
GPU-STOMP: These results are reproduced from the original Matrix Profile II paper - NVIDIA Tesla K80 (contains 2 GPUs) and serves as the performance benchmark to compare against.
STUMP.2: stumpy.stump executed with 2 CPUs in Total - 2x Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20GHz processors parallelized with Numba on a single server without Dask.
STUMP.16: stumpy.stump executed with 16 CPUs in Total - 16x Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20GHz processors parallelized with Numba on a single server without Dask.
STUMPED.128: stumpy.stumped executed with 128 CPUs in Total - 8x Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20GHz processors x 16 servers, parallelized with Numba, and distributed with Dask Distributed.
STUMPED.256: stumpy.stumped executed with 256 CPUs in Total - 8x Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20GHz processors x 32 servers, parallelized with Numba, and distributed with Dask Distributed.
GPU-STUMP.1: stumpy.gpu_stump executed with 1x NVIDIA GeForce GTX 1080 Ti GPU, 512 threads per block, 200W power limit, compiled to CUDA with Numba, and parallelized with Python multiprocessing
GPU-STUMP.2: stumpy.gpu_stump executed with 2x NVIDIA GeForce GTX 1080 Ti GPU, 512 threads per block, 200W power limit, compiled to CUDA with Numba, and parallelized with Python multiprocessing
GPU-STUMP.DGX1: stumpy.gpu_stump executed with 8x NVIDIA Tesla V100, 512 threads per block, compiled to CUDA with Numba, and parallelized with Python multiprocessing
GPU-STUMP.DGX2: stumpy.gpu_stump executed with 16x NVIDIA Tesla V100, 512 threads per block, compiled to CUDA with Numba, and parallelized with Python multiprocessing
Running Tests#
Tests are written in the tests directory and processed using PyTest and requires coverage.py for code coverage analysis. Tests can be executed with:
./test.sh
Python Version#
STUMPY supports Python 3.7+ and, due to the use of unicode variable names/identifiers, is not compatible with Python 2.x. Given the small dependencies, STUMPY may work on older versions of Python but this is beyond the scope of our support and we strongly recommend that you upgrade to the most recent version of Python.
Getting Help#
First, please check the discussions and issues on Github to see if your question has already been answered there. If no solution is available there feel free to open a new discussion or issue and the authors will attempt to respond in a reasonably timely fashion.
Contributing#
We welcome contributions in any form! Assistance with documentation, particularly expanding tutorials, is always welcome. To contribute please fork the project, make your changes, and submit a pull request. We will do our best to work through any issues with you and get your code merged into the main branch.
Citing#
If you have used this codebase in a scientific publication and wish to cite it, please use the Journal of Open Source Software article.
S.M. Law, (2019). STUMPY: A Powerful and Scalable Python Library for Time Series Data Mining. Journal of Open Source Software, 4(39), 1504.
@article{law2019stumpy,
author = {Law, Sean M.},
title = {{STUMPY: A Powerful and Scalable Python Library for Time Series Data Mining}},
journal = {{The Journal of Open Source Software}},
volume = {4},
number = {39},
pages = {1504},
year = {2019}
}
References#
Yeh, Chin-Chia Michael, et al. (2016) Matrix Profile I: All Pairs Similarity Joins for Time Series: A Unifying View that Includes Motifs, Discords, and Shapelets. ICDM:1317-1322. Link
Zhu, Yan, et al. (2016) Matrix Profile II: Exploiting a Novel Algorithm and GPUs to Break the One Hundred Million Barrier for Time Series Motifs and Joins. ICDM:739-748. Link
Yeh, Chin-Chia Michael, et al. (2017) Matrix Profile VI: Meaningful Multidimensional Motif Discovery. ICDM:565-574. Link
Zhu, Yan, et al. (2017) Matrix Profile VII: Time Series Chains: A New Primitive for Time Series Data Mining. ICDM:695-704. Link
Gharghabi, Shaghayegh, et al. (2017) Matrix Profile VIII: Domain Agnostic Online Semantic Segmentation at Superhuman Performance Levels. ICDM:117-126. Link
Zhu, Yan, et al. (2017) Exploiting a Novel Algorithm and GPUs to Break the Ten Quadrillion Pairwise Comparisons Barrier for Time Series Motifs and Joins. KAIS:203-236. Link
Zhu, Yan, et al. (2018) Matrix Profile XI: SCRIMP++: Time Series Motif Discovery at Interactive Speeds. ICDM:837-846. Link
Yeh, Chin-Chia Michael, et al. (2018) Time Series Joins, Motifs, Discords and Shapelets: a Unifying View that Exploits the Matrix Profile. Data Min Knowl Disc:83-123. Link
Gharghabi, Shaghayegh, et al. (2018) “Matrix Profile XII: MPdist: A Novel Time Series Distance Measure to Allow Data Mining in More Challenging Scenarios.” ICDM:965-970. Link
Zimmerman, Zachary, et al. (2019) Matrix Profile XIV: Scaling Time Series Motif Discovery with GPUs to Break a Quintillion Pairwise Comparisons a Day and Beyond. SoCC ‘19:74-86. Link
Akbarinia, Reza, and Betrand Cloez. (2019) Efficient Matrix Profile Computation Using Different Distance Functions. arXiv:1901.05708. Link
Kamgar, Kaveh, et al. (2019) Matrix Profile XV: Exploiting Time Series Consensus Motifs to Find Structure in Time Series Sets. ICDM:1156-1161. Link




